Bayes’ theorem and base rate neglect

By /
Table Of Contents
  1. Introduction
  2. The Math
  3. Bayes' Theorem in Plain English
  4. Bayes Theorem as a Normative Model
  5. Bayes Theorem as a Descriptive Model
  6. Bayes' Theorem and Base Rate Neglect in Casino Gambling

Introduction

Bayes’ theorem (Wikipedia) refers to a probabilistic framework for updating beliefs in light of new evidence. Initially derived from the work of the Reverend (and statistician and philosopher) Thomas Bayes, published in 1763, this theorem provides a formal method for revising prior probabilities based on observed data, thus allowing for the incorporation of new information.

The Math

Skip this if you’re not a probability buff.

In formal mathematical terms, Bayes’ Theorem is given by a relatively straight forward algebraic formula (though in practice applying Bayes’ theorem requires numbers that are rarely easy to come by):

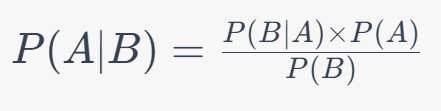
Where:

  • P(A∣B) is the posterior probability (that is, the current, updated probability) of event A occurring, given that event B has occurred.
  • P(B∣A) is the (known) probability of event B occurring given that event A has occurred.
  • P(A) is the prior probability of event A: our initial belief about the probability of event A independent of whether or not B has occurred.
  • P(B) is the marginal likelihood or evidence: This is the probability of event B independent of any evidence about event A occurring.

Bayes’ Theorem in Plain English

Imagine you’re trying to figure out the likelihood that it’s going to rain tomorrow (the probability of A given some evidence, B). You start with an initial likelihood that it’s going to rain, that is, the prior probability, P(A), where A is “it actually rains”. That might be, for example, how often it typically rains this time of year. Let’s imagine P(A) = 0.25 or 25% of the time.

Now, you hear the weather forecast, and they predict rain. This new piece of information is your “evidence“, B (of course, in actual fact, weather predictions usually involve probabilities themselves, but we’re keeping the example simpler by supposing it’s just a “yes” or “no” prediction). Let’s say B = the weather report predicts rain.

To use this evidence with Bayes’ theorem, you also need to consider:

  1. How likely you would hear this forecast if it was indeed going to rain. That P(B|A), the probability that a weather report will have predicted rain, given that it actually does rain. Let’s assume there are not a lot of false positives, that is, that when a weather reporter predicts rain, they usually get it right and it does rain. So let’s say there’s a 0.9 probability or a 90% chance that it actually will rain, given that the weather report said it would. So P(B|A) = 0.9
  2. How often weather forecasts predict rain in general at this time of year, regardless of whether it truly rains or not. This is the general probability of the evidence. That is P(B). Let’s imagine P(B) equals P(A) (they predict rain just as often as it actually does rain this time of year, 25% of the time. It’s important to note that this does not at all indicate they are good at their jobs. They could be wrong 100% of the time, picking their 25% of the days from the 75% of the days when it does not actually rain. P(B) = 0.30. Important not

Using Bayes’ theorem, you combine your prior belief with the new evidence (the forecast) to get an updated belief (or probability) that it will rain tomorrow: P(A|B), the probability that it’s going to rain given that there was a forecast of rain. This updated belief is called the “posterior” probability. That’s the probability you want to know! P(A/B) = (0.9*0.25) / 0.30 = 0.75. There’s a 75% chance it is going to rain given that the weather report said it was going to rain.

Bayes Theorem as a Normative Model

Bayes’ theorem is widely accepted among decision scientists as providing a normative process for decision making under risk or uncertainty. It is central to the leading normative model of rational choice involving decisions under uncertainty, Subjective Expected Utility (SEU) Theory, as it prescribes how to effectively update subjective probabilities given repeated sampling of the environment (with decisions from experience) or when given the probability values necessary to calculate P(A|B) (with decisions from description).

Bayes Theorem as a Descriptive Model

Intuitive Statisticians

Research on decisions from experience, such as work with operant or classical conditioning, suggests that people, like other animals, are impressively effective intuitive statisticians, adjusting probabilities like good Bayesians, at least at the unconscious, biological level.

Base Rate Neglect and Representativeness

Research using decisions from description, however, suggests the opposite. In particular, one of the essential components of Bayes’ theorem are base rates. Base rates are the overall or background probabilities of specific events in a general population. Base rates are an example of the prior probabilities of A and B, that is, P(A) and P(B), from Bayes’ Theorem. In several studies, when research participants are told prior probabilities (that is base rates), they tend to ignore them altogether, what Kahneman & Tversky have called base rate neglect and what might also be referred to as the base rate fallacy or the base rate bias.

For a more intuitive example (distorted from an intro to psychology textbook I can no longer find), consider whether you would think it’s more likely that a person reading poetry in a Prague park is more likely to be a classics professor at an Ivy League university or a truck driver. Students in my statistics class overwhelmingly conclude it would be far more likely that the person is an Ivy League classics professor than a truck driver (even immediately after being taught about base rate neglect). But when I have students estimate the various base rates (how many Ivy League universities are there, how many classics professors would you guess are in the average Ivy League university, how many of them do you think are likely to be in Prague, how often do you think the average classic professor sits in a park reading poetry; now repeat those questions for truck drivers). It quickly becomes clear that—if the students did the math based on their own likelihood estimates—the likelihood is far higher that the person is a truck driver than a professor in an Ivy League university.

For a particularly important example, consider a case where 1 in 1000 people in a population will contract a fatal disease and everyone in the population is given a test for the disease. Imagine the test has a false positive rate of 1% (meaning that–among the people who do NOT have the disease, 1% will nonetheless test positive) and a 99% TRUE positive rate (meaning that among the people who DO have the disease the test will accurately diagnose them 99% of the time. Now, imagine you come in to test for the disease and you test positive. How likely is it that you have the disease?

Most people, including most doctors in much of the research in this domain, will conclude that the probability is 99%. The first clue that this is wrong is to point out that the 1% false positive rate and the 99% true positive rate did not need to add to 100%. They do in this scenario because it contributes to base rate neglect, which is the intention of the example, since the fact the two numbers add to 100% suggests they are complements of each other. In fact the two numbers are independent, generated from two distinct populations, one population that has the disease (the true positive rate) and one population that does not have the disease (the false positive rate). The actual complement for the true positive rate is the false negative group, the percentage of people who DO have the disease who test negative, and who would by definition be 1% given the true positive rate. And the actual complement for the false positive rate are the true negatives, the people from the population without the disease who correctly test negative (who by definition would be 99%, given the 1% false positive rate).

There could just as well be identical false positive and false negative rates, as would be expected from a bogus test that is not influenced by whether or not people have the disease at all. For example, imagine a company is hired to produce a test with a true positive rate of 99% (so that 99% of the time it would correctly catch the disease from a sample of people known to have the disease). They could design a test that randomly tests positive 99% of the time, and that would achieve the goal, accurately identifying people who have the disease 99% of the time. It would also, unfortunately, have a false positive rate of 99% (incorrectly showing 99% of the time that people who do NOT have the disease actually do). Of course, in that case with the bogus test and a base rate in the population of 1 in 1000, there is still one chance in 1000 of each person who takes the test having the disease, despite the fact that the true positive and false positive rates were correct, pointing to the fact that the success and failure rates of the diagnoses are independent of the frequencies in the population and are, in fact, not diagnostic unless you also know, and factor in, those frequencies.

For a number of classic examples of base rate neglect and a step-by step calculation that clarifies where decision makers commonly go astray, see this base rate fallacy Wikipedia article.

Also note that this affect largely disappears when natural frequencies are provided, which take into account base rates. See this well-cited peer-reviewed article for an example of compelling research on the topic, and this target article in the journal Behavioral and Brain Sciences with commentaries from leaders in the field for insight into the complexity of the issue.

Unfortunately, it is not a simple matter to include natural frequencies to help doctors or patients evaluate the likelihood that a test result is correct. One problem is that base rates (that is, population frequencies) vary widely across time and place. Consider how dramatically the frequency of Covid in the population varied in a single region between 2020 and 2023, and how much that differed across regions.

Another problem is that what counts as the relevant population depends entirely on the individual getting tested. People are not randomly selected from a well-defined population to take a test; rather, they tend to get tested because there is some reason they suspect they are positive. In those case, the proper population for taking into account base rates would be other people with the same symptoms or with other matched reasons for suspecting a positive test (pregnant mothers at a specific age who get testing for Down’s syndrome due to their age-related risk factor, for example). While population frequency for those age-specific numbers with a Down’s Syndrome test might be available, in most cases our reasons for getting tested are idiosyncratic. Imagine, for example, the wide variety of initial certainty a person might have when taking a pregnancy test (a woman with morning sickness and a growing belly and no period versus a woman who has not had intercourse and no symptoms). Those problems aside, there can be no denying that a positive test for an illness which affects 50% of the population should be assessed a far higher likelihood of being correct than a positive test for an illness that affects 0.01% of the population (5000 times higher, all other things being equal), and yet even medical doctors often ignore these base rates when advising their patients about test accuracy.

Evidence for base rate neglect has been used as an example of the representativeness heuristic, with the idea that people are attending to the sample probabilities (the evidence) and ignoring the less apparent population frequencies. Of course, this can also be used to support the availability heuristic, since the evidence is arguably more readily available.

The fact that distinct heuristics and biases can be used to explain the same choice has been one of the criticisms of heuristics and biases more generally, as has the observation that the same heuristic or bias can be coopted to explain contrary behaviors (the hot hand and the gambler’s fallacy are an example of that, where the two opposing fallacies have both been explained by representativeness and availability and belief in the law of small numbers). These criticisms aside, representativeness and availability do a great deal to help make sense of base rate neglect.

Bayes’ Theorem and Base Rate Neglect in Casino Gambling

Bayes’ Theorem may occasionally come up in the domain of casino gambling, particularly with reference to slot machines, since they are the dominant game in casinos and they are one of the few games that present likelihoods that seem easy to calculate but where there is almost no relationship between those apparent probabilities and the actual probabilities, and so updating subjective likelihoods from experience is particularly important. The probabilities that each symbol will occur suggested by the design of the physical reels are completely different from the actual probabilities which are programmed into a chip in each slot machine that maps each symbol to very different likelihoods in what is termed the virtual reel. This allows jackpots to reach the millions of dollars. For example, while a reel might show 20 symbols equally spaced that spin and come to a gradual stop, simulating a random chance of 1 in 20 for each symbol (or 1 in 8000 [that is, 20*20*20] for any combination of outcomes, the actual likelihood might be 0.5 (that is a 50% chance) for a non-jackpot cherry symbol and 0.001 (0.1% or one chance in 1,000) for “lucky 7” jackpot symbol (that would be one chance in a billion to get all three 7s).

In fact, each of the three reels can have its own virtual reel or the full combination of three wheels can have a virtual reel assignment, so that it can be relatively common to get a jackpot symbol on two of the reels and similarly common to get “blank” just above or below the jackpot symbol on the third reel (an example of what’s called a “near miss”), yet have there be one chance is 100 million of getting all three jackpot symbols. As long as the virtual reel is itself random, such slot machines are legal in Las Vegas, and there is no requirement for the casinos to provide the true probabilities of different payouts or even to explain that the surface structure is not in fact random.

A Bayesian might suggest that the slot machine players should update their subjective probabilities based on the actual outcomes in the game to reflect the true probabilities of getting a jackpot. Alternatively, a more holistic Bayesian might suggest that given our cumulative experience in real world settings, a strong commitment to base rates based on the surface structure (the design of the physical reels) should require extensive evidence before those probabilities are adjusted by the evidence, since in most domains such a design would be random (as it was in early slot machines) and it takes high-tech design so that the physical reels appear random and in are only random at a virual level.

In actual fact, regular slot machine players all know that the surface structure does not match the virtual structure, and it tends to be novice slot machine players or non-gamblers who do not understand the degree to which the games are designed to misrepresent chance. How those gamblers respond at the level of biological conditioning, however, is a separate question, and it may be that the regular exposure to apparent near misses powerfully affects conditioned responses at the automatic, impulsive level, despite the gamblers being consciously aware that the near misses are a designed fiction. The highly addictive nature of casino slot machines suggest this may be the case, although separating the impact of the near miss from the impact of more basic and demonstrably effective random reinforcement is difficult to do without careful experimental controls that would be hard to justify to an ethics review board.

Scroll to Top